Never trust a computer you can’t throw out a window.
As seen in the previous project, orthographic projection gives a clear visualization of 3D objects on a 2D screen. However, it does not reflect the way we actually see things and so is not as useful in computer graphics applications intended to mimic reality, such as animations or first-person games. Perspective projection is the choice for these cases, as it models objects as we see them in reality, displaying them with perspective, which varies at different viewing angles and positions.
The perspective projection algorithm is similar to orthographic projection. A point in 3D scene space has coordinates and is projected onto the canvas at point , with coordinates . Figure 1 shows point lying on the canvas plane, viewed from the side. Points , , and the camera are colinear and form one side of a triangle. The other two sides are the horizontal plane and the planes perpendicular to the horizontal that contain points and . A set of similar triangles is constructed, as they share three congruent angles.
The value we want to find is , the height of the projected point above the horizontal. is a set constant since the canvas is always the same distance away from the camera (for this project, at least).
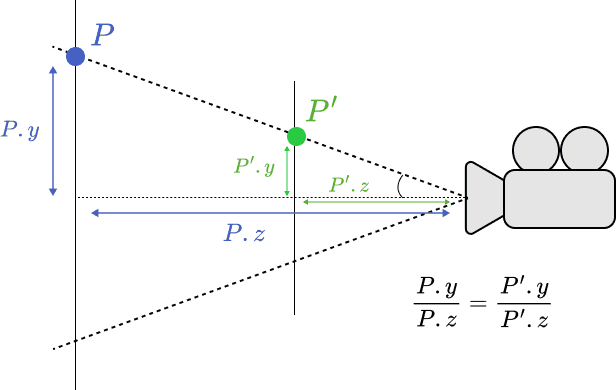 Fig. 1 – Side Diagram of Perspective Projection
Fig. 1 – Side Diagram of Perspective Projection
By the definition of similar triangles, the sides of the two triangles form equal ratios, giving
Solving for gives
There are a few things that must be changed about this relationship before it can be implemented. It makes things easy if we define , which lets us leave it out of the calculation. Additionally, by convention, the camera view points down the negative axis, so we should write instead of . These properties of similar triangles resulting from a projection onto the canvas apply to the coordinates too, where the plane of figure 1 is rotated about the axis. Finally, we can compute the and coordinates of the point to be displayed on the screen:
That’s all that’s needed to make a 3D object projected onto a 2D canvas with perspective projection. I made an array storing coordinates of a cube and drew lines connecting adjacent verticies to create a cube projection. As an added functionality we can introduce another term in the denominator, which we can change with user input.
A larger value of means that the coordinates on the canvas are smaller. We are effectively zooming out by increasing the distance from the camera to in the calculations.
As mentioned in the orthographic projection project, in all mainstream graphics applications, these calculations are performed through matrix multiplication, which can encode other information like transformations and is hardware-optimized. This matrix has a dimension of 4x4, meaning that the 3D coordinates must be expressed with four values. This is accomplished by converting them to homogenous coordinates such that in converting homogenous to Cartesian coordinates, each coordinate is divided by .
Since in perspective projection, obtaining the projected coordinates is done through dividing coordinates by of point , we can set . The coordinates are then multiplied by the matrix and converted back to Cartesian coordinates where they are divided by .
There are many more aspects of perspective projection, including clipping planes, normalizing the coordinate to retain depth information, and changing the field of view. They all stem from the same principles and are extensions of the basic geometry used to find the projected coordinates on the canvas.
For further reading, I suggest Scratchapixel, which goes into more depth and includes the extensions mentioned above.